数组排序方法(数组排序方法详解：算法与优化)

在当今瞬息万变的数据环境中，对海量信息进行有效排序至关重要。数组排序方法是实现这一目标的关键工具，为各种应用程序提供高效的数据组织。

一、冒泡排序

冒泡排序是一种简单但直观的排序算法。它通过重复扫描数组，比较相邻元素，并将较小的元素移动到其正确位置，来对数组进行排序。经过多次扫描后，最大的元素会“浮”到数组的末尾。

尽管冒泡排序易于理解和实现，但其时间复杂度为 O(n^2)，对于大型数组非常低效。

示例：将数组 [5, 3, 1, 2, 4] 冒泡排序：

- 第一轮：将 1 和 2 交换，得到 [5, 3, 2, 1, 4]。

- 第二轮：将 1 和 3 交换，得到 [5, 2, 3, 1, 4]。

- 以此类推，直到数组排序为 [1, 2, 3, 4, 5]。

二、快速排序

快速排序是一种分而治之的排序算法。它选择一个枢轴元素，将数组划分为两个子数组：一个包含小于枢轴元素的元素，另一个包含大于枢轴元素的元素。

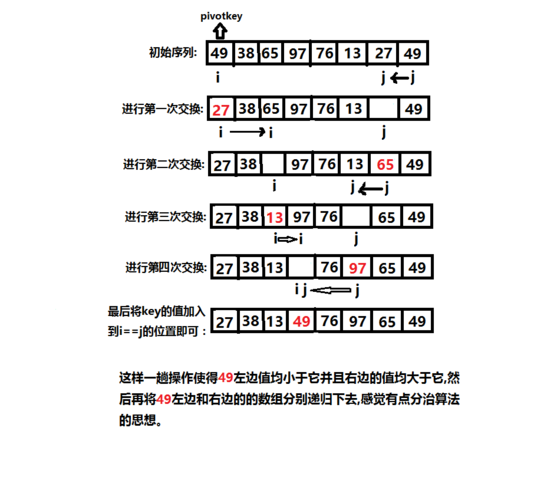
快速排序递归地对这两个子数组进行排序，直到整个数组排序完毕。它的平均时间复杂度为 O(n log(n))，在大多数情况下优于冒泡排序。

示例：将数组 [5, 3, 1, 2, 4] 快速排序：

- 选择枢轴为 3。

- 将数组划分为 [1, 2] 和 [4, 5]。

- 递归地对这两个子数组进行快速排序。

- 合并排序后的子数组，得到 [1, 2, 3, 4, 5]。

三、归并排序

归并排序也是一种分而治之的排序算法。它将数组拆分成越来越小的子数组，直到每个子数组只有一个元素。

算法将相邻的子数组合并为一个排序的子数组，继续合并直到整个数组排序完毕。归并排序的时间复杂度始终为 O(n log(n))，使其成为大型数组的高效排序方法。

示例：将数组 [5, 3, 1, 2, 4] 归并排序：

- 将数组拆分为 [5], [3], [1], [2], [4]。

- 合并 [5] 和 [3] 为 [3, 5]。

- 合并 [1] 和 [2] 为 [1, 2]。

- 合并 [3, 5] 和 [1, 2] 为 [1, 2, 3, 5]。

- 合并 [1, 2, 3, 5] 和 [4] 为 [1, 2, 3, 4, 5]。

四、希尔排序

希尔排序是一种基于插入排序的改进算法。它将数组元素按照一定间隔分组，然后对每个组进行插入排序。

间隔逐渐减小，直到为 1，此时数组完全排序。希尔排序的时间复杂度介于 O(n) 和 O(n^2) 之间，具体取决于间隔的序列。

示例：将数组 [5, 3, 1, 2, 4] 希尔排序：

- 以间隔 2 分组：[5, 2], [3, 4], [1]。

- 对每个组进行插入排序。

- 间隔减小为 1，得到 [1, 2, 3, 4, 5]。

通过了解数组排序方法的优缺点，开发者可以优化其应用程序的性能和效率。选择合适的排序算法可以显著减少数据处理时间，在当今竞争激烈的技术环境中获得竞争优势。

随着数据量的不断增长，有效的数组排序技术变得更加重要。不断研究和创新将带来新的算法和优化技术，进一步提高数据处理能力。